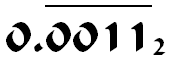Errores de redondeo
Como los números de punto flotante tienen un número de dígitos limitado, no pueden representar todos los números reales de forma precisa: cuando hay más dígitos de los que permite el formato, los que sobran se omiten ─ el número se redondea. Hay tres razones por las que esto puede ser necesario:
- Denominadores grandes En cualquier base, cuanto mayor es el denominador de una fracción (irreducible), más dígitos se necesitan en notación posicional. Un denominador lo suficientemente grande necesitará redondeo, no importa qué base o número de dígitos disponible haya. Por ejemplo, 1/1000 no se puede representar de manera precisa en menos de 3 dígitos decimales, ni ningún múltiplo suyo (que no permita simplificar la fracción).
- Dígitos periódicos Cualquier fracción (irreducible) donde el denominador tenga un factor primo que no esté en la base requiere un número infinito de dígitos que se repiten periódicamente a partir de un cierto punto. Por ejemplo, en decimal 1/4, 3/5 y 8/20 son finitos, porque 2 y 5 son los factores primos de 10. Pero 1/3 no es finito, ni tampoco 2/3 o 1/7 o 5/6, porque 3 y 7 no son factores primos de 10. Las fracciones con un factor primo de 5 en el denominador pueden ser finitas en base 10, pero no en base 2 ─ la mayor fuente de confusión para los principiantes en los números de punto flotante.
- Números no racionales Los números irracionales no se pueden representar como una fracción regular, y en notación posicional (no importa en qué base) requieren un número infinito de dígitos no periódicos.
Métodos de redondeo
Hay varias formas diferentes de redondear, y esto puede ser muy importante en programación, porque el redondeo puede causar problemas en algunos contextos que se pueden solucionar utilizando un método de redondeo distinto. Los más usuales son:
- Redondeo hacia el cero o truncamiento - simplemente se omiten los dígitos sobrantes. Es el método más sencillo, pero introduce más error del necesario y un sesgo hacia el cero cuando se manejan sobre todo números positivos o sobre todo negativos.
- Redondeo al alza - si la fracción truncada es mayor o igual que la mitad de la base, se incrementa el último dígito. Este método es el que se enseña en el colegio normalmente y es el que usa la mayoría de la gente. Minimiza el error, pero también introduce un sesgo (lejos del cero).
- Redondeo mitad al par también conocido como el redondeo del banquero - si la fracción truncada es mayor que la mitad de la base, se incrementa el último dígito. Si es igual a la mitad de la base, se incrementa solamente si el resultado es par. Esto minimiza el error y el sesgo, y por eso se prefiere en contabilidad. Es el método por defecto en el estándar IEEE 754.
Ejemplos en base 10:
| Hacia el cero | Al alza | La mitad al par | |
|---|---|---|---|
| 1.4 | 1 | 1 | 1 |
| 1.5 | 1 | 2 | 2 |
| -1.6 | -1 | -2 | -2 |
| 2.6 | 2 | 3 | 3 |
| 2.5 | 2 | 3 | 2 |
| -2.4 | -2 | -2 | -2 |
Se pueden encontrar más métodos de redondeo (inglés) en la Wikipedia inglesa.
© Publicado en http://puntoflotante.org/ bajo una licencia Creative Commons Atribución Unported (BY). Original en inglés por Michael Borgwardt en http://floating-point-gui.de/.