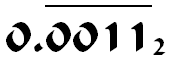Fracciones binarias
Cómo funcionan
Como programador, deberías estar familiarizado con el conceptro de enteros binarios, esto es, la representación de números enteros como series de bits:
| Decimal (base 10) | Binario (base 2) | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ⋅ | 101 | + | 3 | ⋅ | 100 | = | 1310 | = | 11012 | = | 1 | ⋅ | 23 | + | 1 | ⋅ | 22 | + | 0 | ⋅ | 21 | + | 1 | ⋅ | 20 |
| 1 | ⋅ | 10 | + | 3 | ⋅ | 1 | = | 1310 | = | 11012 | = | 1 | ⋅ | 8 | + | 1 | ⋅ | 4 | + | 0 | ⋅ | 2 | + | 1 | ⋅ | 1 |
Así almacenan números internamente los ordenadores. Y para números racionales en notación posicional, hacen lo mismo:
| Decimal (base 10) | Binario (base 2) | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6 | ⋅ | 10-1 | + | 2 | ⋅ | 10-2 | + | 5 | ⋅ | 10-3 | = | 0.62510 | = | 0.1012 | = | 1 | ⋅ | 2-1 | + | 0 | ⋅ | 2-2 | + | 1 | ⋅ | 2-3 |
| 6 | ⋅ | 1/10 | + | 2 | ⋅ | 1/100 | + | 5 | ⋅ | 1/1000 | = | 0.62510 | = | 0.1012 | = | 1 | ⋅ | 1/2 | + | 0 | ⋅ | 1/4 | + | 1 | ⋅ | 1/8 |
Problemas
Aunque funcionan igual en principio, las fracciones binarias son diferentes a las fracciones decimales en qué números que se pueden representar con precisión dado un número de dígitos, y por tanto también en qué números resultan en errores de redondeo: concretamente, en binario solo se pueden representar como una fracción finita aquellos números en los que el denominador es una potencia de 2. Por desgracia, esto no incluye la mayoría de los números que pueden ser representados como una fracción finita en base 10, como 0.1.
| Fracción | Base | Notación posicional | Redondeado a 4 dígitos | Valor redondeado como fracción | Error de redondeo |
|---|---|---|---|---|---|
| 1/10 | 10 | 0.1 | 0.1 | 1/10 | 0 |
| 1/3 | 10 | 0.3 | 0.3333 | 3333/10000 | 1/30000 |
| 1/2 | 2 | 0.1 | 0.1 | 1/2 | 0 |
| 1/10 | 2 | 0.00011 | 0.0001 | 1/16 | 3/80 |
Y así es como ya obtienes un error de redondeo con solamente escribir un número como 0.1 y pasarlo por tu intérprete o compilador. No es tan grande como 3/80 y puede ser invisible porque los ordenadores cortan después de 23 o 52 dígitos binarios en vez de 4. Pero el error está ahí y causará problemas eventualmente si simplemente lo ignoras.
¿Por qué usar binario?
En el nivel más inferior, los ordenadores están basados en miles de millones de elementos eléctricos que tienen dos estados (normalmente baja y alta tensión). Interpretándolos como 0 y 1, es muy fácil construir circuitos para almacenar números binarios y hacer cálculos con ellos.
Mientras que es posible simular el comportamiento de los números decimales con circuitos binarios también, es menos eficiente. Si los ordenadores usaran números decimales internamente, tendrían menos memoria y serían más lentos con el mismo nivel de tecnología.
Puesto que la diferencia de comportamiento entre números binarios y decimales no es importante para la mayor parte de las aplicaciones, la elección lógica es construir ordenadores basados en el sistema binario y vivir con el hecho de que hay que poner un poco más de atención y esfuerzo para las aplicaciones que tienen que funcionar como un número decimal.
© Publicado en http://puntoflotante.org/ bajo una licencia Creative Commons Atribución Unported (BY). Original en inglés por Michael Borgwardt en http://floating-point-gui.de/.