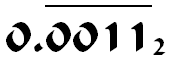Respuestas básicas
¿Por qué al sumar mis números, como 0.1 + 0.2, en vez de dar 0.3 da un resultado extraño como 0.30000000000000004?
Porque internamente, los ordenadores usan un formato (punto flotante binario) que no puede representar de forma precisa números como 0.1, 0.2 o 0.3 de ninguna manera.
Cuando el código es compilado o interpretado, tu “0.1” se redondea al número más cercano en ese formato, lo que resulta en un pequeño error de redondeo incluso antes de que se haga la operación.
¿Por qué los ordenadores usan un sistema tan estúpido?
No es estúpido, solo diferente. Los números decimales no pueden representar con precisión un número como ⅓, así que lo tienes que redondear a algo como 0.33 ─ y no esperas que 0.33 + 0.33 + 0.33 sea igual a 1 tampoco, ¿no?
Los ordenadores usan números binarios porque son más rápidos de manejar, y porque para la mayoría de operaciones un error en la 17ª cifra decimal no importa en absoluto ya que los valores con los que trabajas no eran así de precisos de todas formas.
¿Qué puedo hacer para evitar este problema?
Eso depende del tipo de cálculos que estés haciendo.
- Si de verdad necesitas que tus resultados se sumen con exactitud, especialmente cuando trabajas con dinero: utiliza un tipo de datos decimal especial.
- Si es solo que no quieres ver todos esos decimales extra: simplemente da formato a tu resultado redondeando a un número fijo de cifras decimales cuando lo presentes.
- Si no tienes un tipo de datos decimal, una alternativa es trabajar con enteros, e.g. hacer todos los cálculos con dinero en céntimos. Pero esto requiere más trabajo y tiene algunas desventajas.
¿Por qué otros cálculos como 0.1 + 0.4 sí funcionan bien?
En este caso, el resultado (0.5) sí puede ser representado de manera exacta como un número de punto flotante, y es posible que los errores de redondeo de los datos de partida se cancelen entre sí ─ aunque no se debería confiar excesivamente en esto (e.g. cuando esos dos números fueron almacenados en representaciones de punto flotante de diferente tamaño, los errores de redondeo pueden no cancelarse entre ellos).
En otros casos como 0.1 + 0.3, el resultado no es realmente 0.4, pero está lo suficientemente cerca como para que 0.4 sea el número más corto que está más cerca del resultado que cualquier otro número de punto flotante. La mayoría de lenguajes presentan ese número en vez de convertir el resultado real a una fracción decimal.
Si quieres más información, puedes acudir a las Referencias.
© Publicado en http://puntoflotante.org/ bajo una licencia Creative Commons Atribución Unported (BY). Original en inglés por Michael Borgwardt en http://floating-point-gui.de/.